
一次方程式 連立方程式 ルートの計算
基本は二次関数や二次方程式と考えは同じですが、対数関数ならではの注意点に気をつけましょう。 31対数の問題①〜対数方程式と対数不等式〜 (1)方程式log 2 xlog 2 (5x)=2 を解け。 例えば次の式は分母にルートが入っていて見栄えが少し悪いです。 $$\frac{3}{\sqrt{5}}$$ この式の分母をなんとかしてルートがない形にしたいわけですがどうしたら良いでしょうか。 これはルートの意味に戻ると同じルートのかけ算は中の数字が出てきますから
一次式とは ルート
一次式とは ルート-あなたは、数学は得意ですか? そのまま勉強していくことで、合格点を取ることができるでしょうか? もしこの質問の答えに「はい!」と大きな声で答えれるのであれば、この記事は見る必要はありません。 ですが、 「今の自分の数学の勉強法に自信がない・・・」 「数学が苦手で点数が近似式と次元 ここで一度, これまでの近似計算に用いていた \( x \) の次元について考えてみよう もし, \( x \) が次元を持っていたとすると, \( x^2 \) などは \( x \) と異なる次元を持つ量である

平方根をつかった二次方程式の解き方の3つのステップ Qikeru 学びを楽しくわかりやすく
今回はベクトルの1次独立と1次従属を解説していくよ! 頑張ってついていきます! さて、今回はベクトルの1次独立と1次従属についてです。 少し聞き慣れない言葉かもしれませんが、ベクトルの足し算やかけ算を使ったあまり難しい内容ではないので安心してください。 一次不等式の解き方 不等式の右辺にある変数を左辺にすべて移行をしたとき、左辺の次数が1になる不等式のことを 一次不等式 といいます。 例えば、 x 2 > 0 x 2 > 0 や −2y 7 ≦ y− 1 − 2 y 7 ≦ y − 1 は一次不等式です。 一方、 x2 2x < 3 x 2 2 x < 3 や √証明は展開すれば分かるので省略.ここでは次の点に注意したい. 例えば (x5) (x3)=x2 8 x 15 などとする. また, (x5a) (x3a)=x2 8a x 15a 2 などとする. さらに, (xa3) (xa2)=x2 (2a5) x (a 2 5a6) などとする. この公式は「総当たりで全部掛ける」というの
足し算と引き算 ルート(平方根)の足し算や引き算を計算するには、ルートの中が同じ数どうしを、分配法則を使ってまとめます。 次の例題を解いてみましょう。 2√5 4√5 2 5 4 5 を計算せよ。 この式のルートの部分は、 √5 5 で共通なので、これに ・上記の理由から、双曲線の式と楕円の式の導出はよく似ているので、要注意! ・次回は、二次曲線の応用に入っていきます。 二次曲線シリーズと関連記事一覧 第1回:「二次曲線と円錐の関係・そして放物線」 第2回:「双曲線の式の導き方とそのグラフ」 最初の判別式では、xの方程式が実数解をもつという条件をしらべます とかけますね 問題はxyの一次式になるのだから、ルートの中身は完全平方でないといけません すると丁度、判別式が0、重解を持つことが条件となります。
一次式とは ルートのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 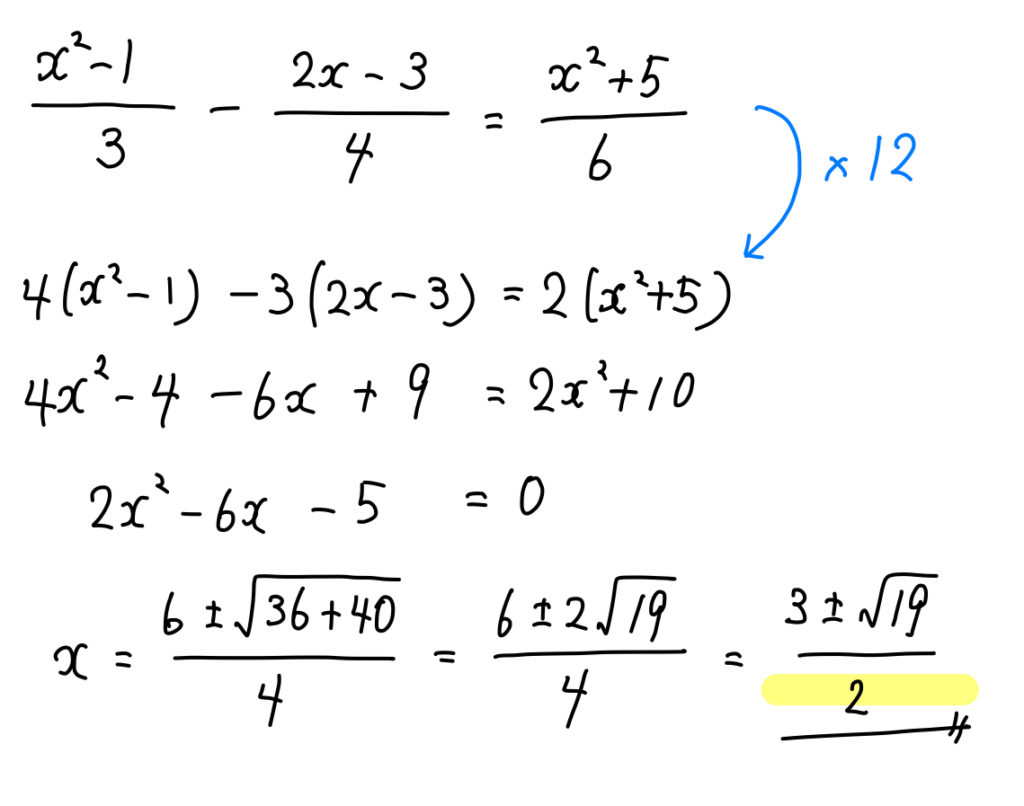 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
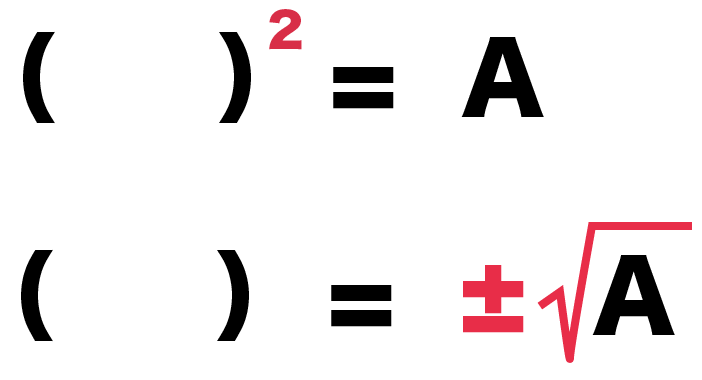 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
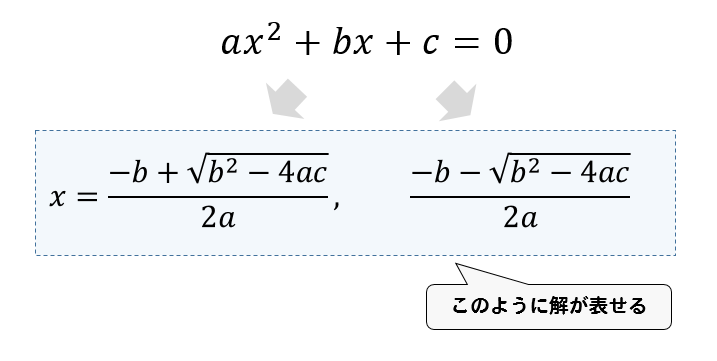 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 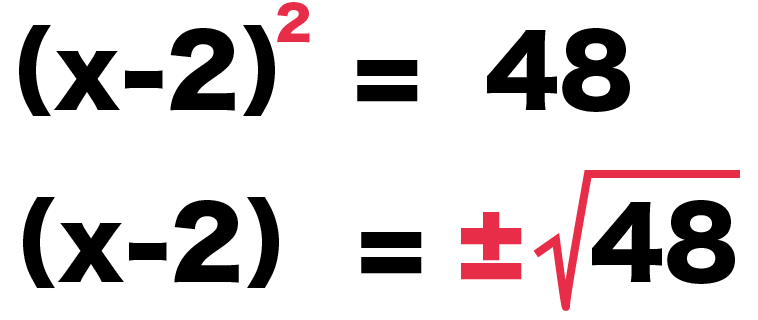 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 | 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
 二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |  二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学 |
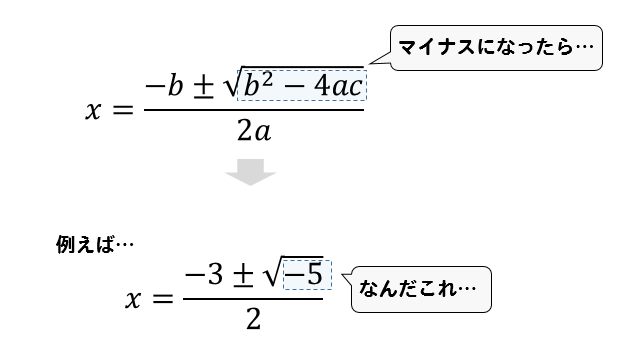
ルートの中身はいちばん簡単にすべきだからね。 例題の計算をみてみると・・・ ・・・ん!? (2)のルートはもっと簡単にできそうじゃないか?? 中身の147を素因数分解すると、 147 = 3×7の2乗 になってる。 因数の7が2乗になってるじゃん??このページでは、中学校学習レベルの数式を英語で読む方法をご説明しています。 2次方程式 $ ax^2bxc=0 $ や、その解の公式 $ x=\frac{b \pm \sqrt{b^2 4ac}}{2a} $ のような文字式、ルート、累乗を含む式って英語でなんて言えばいいんだろう そんな疑問をこのページで解決しましょう!





0 件のコメント:
コメントを投稿